آنالیز واریانس یا تحلیل واریانس یکی از روش های پرکاربرد آماری است. هدف اصلی این روش آماری، مقایسه میانگین های چند گروه مستقل، در متغیر وابسته مورد نظر است. علاوه بر این، در تحلیل واریانس دو و چند راهه، روابط تعاملی بین متغیرهای مستقل، بر متغیر وابسته مورد بررسی قرا می گیرد.
در این مقاله مطالبی در زمینه مباحث زیر ارائه شده است
- کاربرد تحلیل واریانس در تحقیقات آزمایشی
- سایر کاربردهای آنالیز واریانس
- انواع تحلیل واریانس
- طبقه بندی تحلیل واریانس براساس تعداد متغیرهای مستقل
- طبقه بندی آنالیز واریانس براساس تعداد متغیرهای وابسته
کاربرد تحلیل واریانس در تحقیقات آزمایشی
آنالیز واریانس در تحقیقات توصیفی از نوع علّی-مقایسه ای کاربرد دارد. علاوه بر این در تحقیقات آزمایشی، برای بررسی تأثیر متغیر مستقل بر متغیر وابسته، می توان از تحلیل واریانس استفاده کرد.
به عنوان مثال، اگر ما قصد داشته باشیم، تأثیر سه روش آزمایشی، در افزایش اعتماد به نفس دانش آموزان را با هم مقایسه کنیم. می توانیم ابتدا، هر یک از روش های آزمایشی بر روی یک گروه مستقل از دانش آموزان، اجرا نماییم. سپس یک آزمون معتبر اعتماد به نفس، برروی سه گروه اجرا نمایم. ودر آخر با استفاده از روش آنوا، میانگین های اعتماد به نفس سه گروه را با هم مقایسه کنیم. تا مشخص کنیم که اولا آیا میانگین اعتماد به نفس این سه گروه با یکدیگر تفاوت معنی دار دارد یا خیر؟ و ثانیا اگر تفاوت وجود دارد، به لحاظ آماری، کدام میانگین ها بیشتر است؟ یعنی در واقع کدام روش ها مؤثرتر است؟
نمونه ای از نتایج آنالیز واریانس یک راهه یا آنوا در تحقیقات آزمایشی در تصویر زیر ارائه شده است.
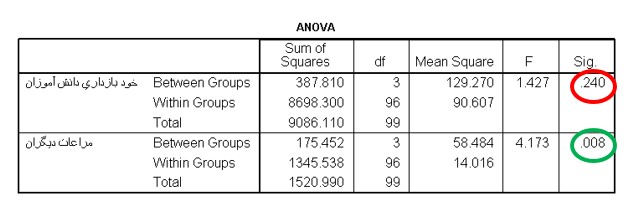
براساس جدول بالا، سطح معنی داری( sig) در متغیر خود بازداری از 0.05 بیشتر است. پس معنی دار نیست. ولی در متغیر مراعات دیگران از 0.05 کمتر است. بنابراین معنی دار است. به این معنی که آزمایش مربوطه در خودبازداری دانش آموزان موثر نبوده است. ولی در بهبود رفتار مراعات دیگران آنها موثر بوده است.
البته، کار به همین سادگی نیست. برای بررسی، تأثیر روش های آزمایشی، غالبا از روش های پیشرفته تر در زیر مجموعه تحلیل واریانس، مثل تحلیل کواریانس یک متغیره یا چند متغیره و در بسیاری از مواقع، از روش اندازه گیری های مکرر استفاده می شود .
سایر کاربردها آنالیز واریانس
استفاده از روش، آنالیز واریانس، محدود به موقعیت های آزمایشی نیست. بلکه هر جا که مقایسه آماری میانگین چند گروه مستقل مد نظر باشد، می توان از این روش استفاده کرد. مثلا، می توان برای مقایسه میانگین قد یا وزن افراد سه منطقه از یک شهر، یا مقایسه میانگین بارندگی سالانه پنج شهر، نیز مقایسه میزان علاقه افراد به چهار فیلم مختلف، مقایسه میزان قند خون چند گروه سنی و …. از روش آنوا استفاده کرد. نکته مهم این است که متغیری که میانگین آن را با هم مقایسه می کنیم، باید دارای مقیاس فاصله ای باشد. و در صورتی که مقیاس مورد نظر رتبه ای بود، بهتر است از روش های ناپارامتریک، مثل روش کروسکال والیس استفاده نماییم.
انواع تحلیل واریانس
تحلیل واریانس را براساس تعداد متغیرهای مستقل و نیز تعداد متغیر وابسته به انوع مختلفی طبقه بندی می کنند.
طبقه بندی تحلیل واریانس براساس تعداد متغیرهای مستقل
تحلیل واریانس، با توجه به تعداد متغیرهای مستقل و وابسته مورد استفاده، انواع مختلفی دارد. اگر تنها یک متغیر مستقل در تحلیل واریانس داشته باشیم، به آن تحلیل واریانس یکطرفه یا یک راهه (آنوا) گفته می شود. اگر دو متغیر مستقل داشته باشیم، آنالیز واریانس، دو راهه یا دو طرفه است و به همین ترتیب، براساس تعداد متغیرهای مستقل، تحلیل واریانس سه راهه، چهار راهه و بالاتر داریم که به طور کلی، به آنها تحلیل واریانس چندطرفه یا چند راهه یا مانوا گفته می شود. البته اگر تعداد متغیرها بیشتر از سه یا چهار متغیر باشد، بهتر است از روش تحلیل رگرسیون خطی استفاده کنیم. در تصویر ذیل نمونه ای از نتایج تحلیل واریانس دو راهه ارائه شده است.
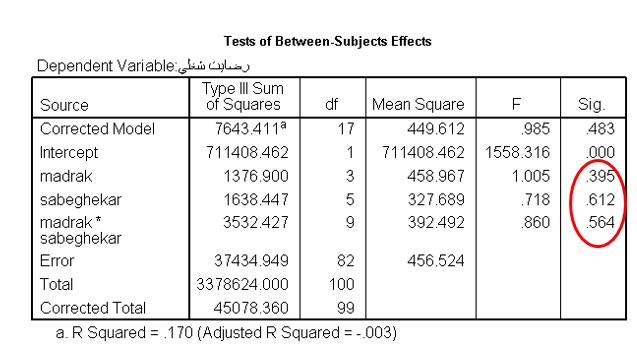
براساس جدول بالا، سطوح معنی داری( sig)، تأثیر متغیر های مدرک تحصیلی و سابقه کار و نیز تعامل این دو متغیر بر رضایت شغلی، از 0.05 بیشتر است. پس معنی دار نیست. با توجه به این نتیجه می توان گفت، متغیرهای مدرک تحصیلی و سابقه کار، تأثیری در رضایت شغلی کارکنان نداشته اند. نیز رابطه تعاملی مدرک تحصیلی و سابقه کار، بر رضایت شغلی موثر نبوده است.
طبقه بندی آنالیز واریانس براساس تعداد متغیرهای وابسته
نیز براساس تعداد متغیرهای وابسته، آنالیز واریانس، به انواعی مثل تحلیل واریانس یک متغیره، دو متغیره و … و در واقع چند متغیره، دسته بندی می کنند. در تحلیل واریانس اگر حذف اثر متغیرهای مزاحم مد نظر باشد به روش مربوطه، تحلیل کواریانس می گویند. و اگر بخواهند، اثر آزمایش را در بستر زمان بررسی کنند و چند مرحله آزمون را با هم مقایسه کنند، از روش اندازه گیری های مکرر استفاده می کنند. در تصویر ذیل نمونه ای از تحلیل کواریانس ارائه شده است.
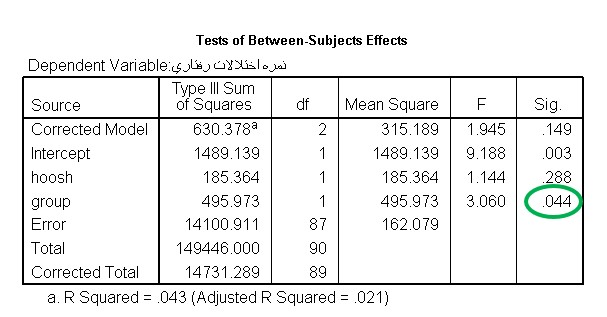
جدول بالا نمونه ای از نتایج تحلیل کواریانس را نشان می دهد. در این تحلیل ابتدا یک روش درمانی برای کاهش اختلات رفتاری اجرا شده است. این روش، بر روی یک گروه آزمایش، از کودکان بیش فعال اجرا شده است. در نهایت نمره اختلات رفتاری گروه آزمایش با یک گروه کنترل با هم مقایسه شده است. در این تحلیل از نمره هوشبهر، به عنوان متغیر مزاحم استفاده شده است. براساس جدول بالا، بعد از حذف، اثر متغیر مزاحم هوشبهر، هنوزتأثیر متغیر گروه (آزمایش و کنترل)، بر اختلات رفتاری معنی دار است. زیرا سطح معنی داری آن (sig) از 0.05 کمتر است. به این معنی که بعد از حذف اثر متغیر مزاحم، هنوز روش درمانی مورد نظر، بر اختلالات رفتاری موثر بوده است.