آنالیز واریانس چند راهه
آنالیز واریانس چند راهه روشی مفید و پرکاربرد، در تحقیقات توصیفی، آزمایشی و شبه آزمایشی است. برای بررسی تأثیر تعاملی متغیرهای مستقل(پیش بین) بر متغیر وابسته(ملاک) از روش آنالیز واریانس چندراهه استفاده می شود. در این نوع از تحلیل، از دو یا چند متغیر مستقل و از یک متغیر وابسته استفاده می شود.
معرفی آنالیز واریانس چند راهه
آنالیز واریانس چند راهه، نوعی تحلیل واریانس است که در آن دو یا چند متغیر مستقل وجود دارد. در این نوع تحلیل واریانس، اگر تعداد متغیرهای مستقل دو تا باشد، به آن، تحلیل واریانس دو راهه می گویند. و اگر سه متغیر مستقل داشته باشیم، تحلیل واریانس سه راهه یا سه طرفه است. و به همین ترتیب، تحلیل واریانس، براساس تعداد متغیرهای مستقل، نام گذاری می شود.
در آنالیز واریانس چند راهه، میانگین متغیر وابسته در هر یک ازسطوح متغیرهای مستقل، با هم مقایسه می شود. این قسمت، شبیه تحلیل واریانس یک راهه است. نیز در تحلیل واریانس چند راهه، تأثیر روابط تعاملی متغیرهای مستقل، بر متغیر وابسته بررسی می شود. این قسمت تفاوت اصلی تحلیل واریانس یک راهه و چند راهه را نشان می دهد. زیرا در تحلیل واریانس یک راهه روابط تعاملی بررسی نمی گردد.
در ادامه دو نمونه از آنالیز واریانس چندراهه یعنی تحلیل واریانس دوراهه و سه راهه را معرفی خواهیم کرد.
آنالیز واریانس چند راهه ( نوع دو راهه)
تحلیل واریانس دو راهه یا دو طرفه، شامل دو متغیر مستقل و یک متغیر وابسته می باشد. در این نوع تحلیل واریانس، تأثیر دو متغیر مستقل بر متغیر وابسته مورد بررسی قرار می گیرد. در این نوع تحلیل، ابتدا آزمودنی ها، براساس دو صفت، یا دو روش آزمایشی، گروه بندی می شوند. به عنوان مثال محققی قصد دارد تأثیر دو متغیر مستقل جنسیت و وضعیت تأهل را بر روی یک متغیر وابسته مسئولیت پذیری، مورد ارزیابی قرار دهد. در این بررسی او می تواند از تحلیل واریانس دو راهه استفاده نماید.
او ابتدا آزمودنی های خود را براساس دو متغیر مستقل جنسیت و وضعیت تأهل به چهار گروه تقسیم می کند. گروه های مورد نظر، به شرح جدول ذیل است. زنان مجرد، زنان متأهل، مردان مجرد و مردان متأهل. در هر گروه 15 نفر آزمودنی و در مجموع 60 نفر ازمودنی در این تحقیق شرکت دارند.
جدول شماره 1

در این تحقیق، با انجام آنالیز واریانس دو راهه، سه فرضیه مورد آزمون قرار می گیرند. اولین فرضیه مربوط به تفاوت آزمودنی های مرد نسبت به آزمودنی ها زن در متغیر مسئولیت پذیری می باشد. دومین فرضیه، تفاوت مسئولیت پذیری آزمودنی های مجرد نسبت به آزمودنی های متأهل را نشان می دهد.
سومین فرضیه، تأثیری تعاملی دو متغیر جنسیت و وضعیت تأهل، بر متغیر مسئولیت پذیری را مورد بررسی قرار می دهد. در این رابطه تعاملی، ممکن است به این نتایج برسیم. مثلا، مسئولیت پذیری مردان متأهل، نسبت به سه گروه دیگر، بیشتر است. یا مسئولیت پذیری زنان مجرد، کمتر از سایر گروه ها، یا کمتر از یکی دیگر از گروه ها است. و مشابه این نتایج.
آنالیز واریانس دو راهه در تحقیقات آزمایشی
تحلیل واریانس دو طرفه، مختص تحقیقات علّی-مقایسه ای، مشابه آنچه در قسمت بالا شرح دادیم نیست. در حقیقت، کاربرد اصلی، آنالیز واریانس دو و چند راهه در تحقیقات آزمایش و شبه آزمایشی است. این روش، در رشته هایی که تأثیر روش های گوناگون بر یک متغیر وابسته را بررسی می کنند، می تواند کاربرد داشته باشد. به عنوان مثال، در رشته هایی مثل پزشکی یا روانشناسی، می توان با استفاده از تحلیل واریانس دو راهه، تأثیر دو دارو یا دو روش درمانی، در بهبود یک بیماری یا یک اختلال رفتاری را مورد ارزیابی قرار داد.
نمونه ای از آنالیز واریانس دو راهه در یک تحقیق آزمایشی
به عنوان نمونه، یک محقق در زمینه روانشناسی، قصد دارد، به طور همزمان تأثیر دو روش شناخت درمانی و رفتار درمانی را در کاهش بیش فعالی، مورد ارزیابی قرار دهد. او ابتدا، چهل نفر از کودکان بیش فعال، را انتخاب می کند. سپس یک آزمون یا چک لیست معتبر از علائم بیش فعالی، بر روی همه آنها ، اجرا می کند. به این آزمون که قبل از اجرای روش های آزمایشی اجرا می شود، پیش آزمون می گویند.
در ادامه، آزمودنی ها را مطابق جدول ذیل، به چهار گروه 10 نفره، تقسیم بندی می کند. و روش های درمانی را بر روی آنها اجرا می کند.
جدول شماره 2
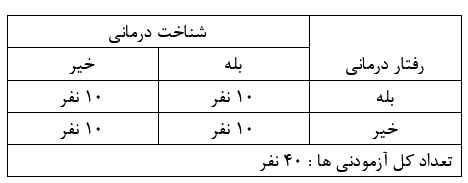
بر روی گروه اول هر دو روش شناخت درمانی و رفتار درمانی، به طور همزمان اجرا می گردد. بر روی گروه دوم، فقط روش رفتار درمانی را اجرا می کند. بر روی گروه سوم فقط روش شناخت درمانی اجرا می شود. و بر روی گروه چهارم، هیچگونه درمانی، اجرا نمی شود. اصطلاحاً، به گروه چهارم که هیج آزمایشی را دریافت نمی دارد، گروه کنترل یا گواه می گویند.
بعد از اجرای روش های درمانی، محقق مجددا آزمون یا چک لیست معتبر از علائم بیش فعالی، که قبلا اجرا شده بود، بر روی هر چهار گروه، اجرا می کند. به این آزمون که بعد از اجرای روش های آزمایشی اجرا می شود، پس آزمون می گویند.
محاسبه نمرات اختلافی
محقق، برای شروع عملیات آماری بر روی نمرات بیش فعالی، ابتدا تفاوت نمرات پیش آزمون و پس آزمون بیش فعالی را برای هر آزمودنی، محاسبه می کند. به این نمرات، که حاصل تفاوت دو مرحله آزمون است، نمرات اختلافی گفته می شود.
استفاده از نمرات اختلافی، بیشتر مناسب تحقیقات آزمایشی است. به شرط آن که نمرات پیش آزمون و پس آزمون، در اختیار محقق باشد. در غیر این صورت، می توان، از نمره پس آزمون، به جای نمرات اختلافی، استفاده کنیم. در ضمن، در تحقیقات علی و مقایسه ای، لزومی به استفاده از نمرات اختلافی وجود ندارد.
تحلیل واریانس دو راهه، بر روی این نمرات انجام می شود. در واقع، محقق در SPSS، در قسمت انجام تحلیل واریانس دو راهه، از این نمرات اختلافی، به عنوان متغیر وابسته استفاده می کند. و از دو متغیر گروه بندی شده، شناخت درمانی و رفتار درمانی، به عنوان متغیرهای مستقل استفاده می شود.
نتایج تحلیل واریانس دو راهه
بعد از انجام این تحلیل واریانس دو راهه، محقق، با توجه به نتایج حاصله، قبول یا رد سه فرضیه را مورد آزمون قرار دهد. نتایج مربوطه در جدول ذیل ارائه شده اند.
جدول شماره 3
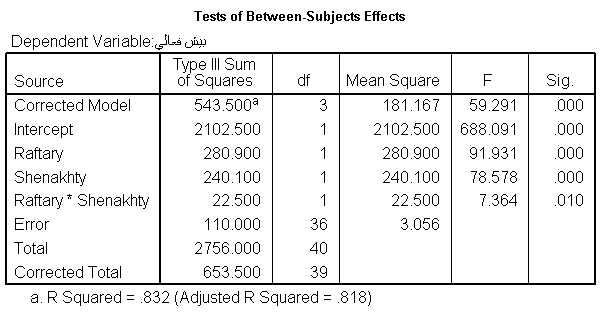
اولین فرضیه، نشان دهنده تأثیر رفتار درمانی، در کاهش بیش فعالی است. در واقع، در این فرضیه میانگین کاهش بیش فعالی، افرادی که رفتار درمانی دریافت کردند و کسانی که این درمان را دریافت نکردند، با هم مقایسه می شود. با توجه به جدول بالا سطح معنی داری (sig)، تأثیر رفتار درمانی صفر و بنابراین از 0.05 کمتر است. این نتیجه نشان دهنده آن است که تأثیر رفتار درمانی بر کاهش بیش فعالی، معنی دار بوده است. اگر سطح معنی داری بیشتر از 0.05 باشد، نشان دهنده آن است که رفتار درمانی تأثیر معنی داری بر کاهش بیش فعالی ندارد.
دومین فرضیه، مربوط به تأثیر شناخت درمانی، در کاهش بیش فعالی است. که تفسیر نتایج مربوطه دقیقا شبیه آنچه در بالا درباره رفتار درمانی گفتیم می باشد.
سومین فرضیه، تأثیر تعاملی دو روش رفتار درمانی و شناخت درمانی، در کاهش بیش فعالی را مورد بررسی قرار می دهد. در واقع، میانگین کاهش بیش فعالی چهار گروه، که در جدول شماره 2 آوردیم، با هم مقایسه می شود. با توجه به جدول شماره 3، سطح معنی داری (sig)، تعامل روش شناختی-رفتاری، در کاهش بیش فعالی، برابر 0.01 است. بنابراین از 0.05 کمتر است و معنی دار است.
با توجه به معنی دار بودن این تأثیر تعاملی، لازم است محقق، برای بررسی دقیق نتایج، از آزمون های تعقیبی استفاده نماید. در این بررسی ممکن است محقق، به این نتیجه برسد که استفاده همزمان از دو روش شناخت درمانی و رفتار درمانی، نسبت به استفاده از یکی از این دو روش، تأثیر بیشتری در کاهش بیش فعالی دارد.
آنالیز واریانس چند راهه (نوع سه راهه)
تحلیل واریانس سه راهه نیز شبیه تحلیل واریانس دو راهه است. تفاوت این دو روش در موارد زیر است. الف) در تحلیل واریانس دو راهه، دو متغیر مستقل داریم ولی در تحلیل واریانس سه راهه، سه متغیر مستقل وجود دارد. ب) تعداد گروه ها در تحلیل واریانس دو راهه، چهار گروه است. ولی در تحلیل واریانس سه راهه، هشت گروه داریم. پ) در تحلیل واریانس دو راهه، به طور همزمان، سه فرضیه مورد آزمون قرار می گیرد. ولی در تحلیل واریانس سه راهه، همزمان، هفت فرضیه مورد آزمون قرار می گیرد.
مثالی از آنالیز واریانس سه راهه
به عنوان مثال اگر محققی، بخواهد تأثیر سه متغیرمستقل A و B و C ، بر متغیر وابسته را بررسی کند. و نیز روابط تعاملی این سه متغیر، بر متغیر وابسته، مد نظر او باشد، باید از تحلیل واریانس سه راهه استفاده نماید.
محقق ابتدا هشت گروه از آزمودنی ها را تشکیل می دهد. شامل گروه های ذیل: گروه کنترل، گروه A، گروه B، گروه C، گروه AB، گروه AC، گروه BC و گروه ABC. گروه کنترل هیچ آزمایشی را دریافت نمی کند. سه گروه یعنی A و B و C تنها یک روش آزمایشی دریافت می دارند. سه گروه دیگر یعنی AB و AC و Bc، به طور همزمان دو روش آزمایشی بر روی آنها اجرا می شود. و یک گروه یعنی گروه ABC، همزمان سه روش آزمایشی بر روی آنها اجرا می شود.
بعد از اجرای روش های آزمایشی، محقق، با استفاده از نمرات اختلافی، یا با استفاده از نمرات پس آزمون، تحلیل واریانس سه راهه را انجام می دهد. نتایج این تحلیل واریانس، هفت فرضیه را مورد آزمون قرار می دهند.
فرضیات مورد بررسی در تحلیل واریانس سه راهه
این هفت فرضیه تأثیر متغیرهای مستقل یا تعامل آنها بر متغیر وابسته را نشان می دهند. و عبارتند از : تأثیر متغیر A، تأثیر متغیرB، تأثیر متغیر C، تأثیر تعامل متغیرهای AوB، تأثیر تعامل متغیر های A وC، تأثیر تعامل متغیرهای B و C، تأثیر تعامل متغیرهای A وB وC.
تفسیر نتایج مربوطه، شبیه تحلیل واریانس دو راهه است. یعنی سطح معنی داری (sig)، هر کدام از تأثیرات، کمتر از 0.05 باشد، معنی دار است و در غیر این صورت معنی دار نیست. در صورت معنی دار شدن هر کدام از تأثیرات، لازم است محقق با استفاده از آزمون های تعقیبی، علت معنی دار شدن تأثیر مربوطه را بررسی نماید تا به نتایج روشن و واضح تری، از آنچه بر اثر آزمایش ها رخ داده است، دست یابد.
عالی بود.ممنون