تحلیل کواریانس

تحلیل کواریانس یا آنکوا، یکی از روشهای بسیار پرکاربرد و مفیداست. در تحقیقات آزمایشی، این روش، کاربرد فراوان دارد. حذف اثر متغیر های همپراش، از امتیازات مهم تحلیل کواریانس بر روشهای تحلیل واریانس،  tوابسته و t اختلافی می باشد. محققین، با استفاده از تحلیل کواریانس، با اطمینان می توانند، تأثیر روش آزمایشی خود را مورد ارزیابی قرار دهند.

معرفی تحلیل کواریانس

کاربرد اصلی تحلیل کواریانس در تحقیقات آزمایشی است، ولی در تحقیقات علّی نیز می توان از این روش استفاده کرد. تحلیل کواریانس، میانگین دو یا چند گروه مستقل، در متغیر یا متغیرهای وابسته را مورد مقایسه قرار می دهد. این روش در عین حال که این مقایسه را انجام می دهد، تأثیر متغیر یا متغیر های مزاحم یا همپراش را حذف می کند. بنابراین، شرط اساسی استفاده از تحلیل کواریانس، وجود متغیر های مزاحم، قابل اندازه گیری است. در تحقیقات آزمایشی، غالبا از پیش آزمون، به عنوان متغیر مزاحم یا همپراش، استفاده می شود. ولی ممکن است محقق، از متغیرهای دیگری که احتمال می رود نتایج آزمایش او را تحت تأثیر قرار دهند، استفاده کند.

به عنوان مثال یک محقق روانشناس را در نظر بگیرید، که در زمینه افزایش اعتماد به نفس دانش آموزان، آزمایشاتی را انجام می دهد. او ممکن است، استدلال کند که هوش دانش آموزان، یک متغیر همپراش است که ممکن است، تأثیر آزمایش را تحت تأثیر قرار دهد و آن را نامعتبر سازد. بنابراین باید هوشبهر دانش آموزان را با ابزاری معتبر، اندازه گیری کند و از نمرات هوشبهر به عنوان متغیر مزاحم استفاده نماید.

نمونه ای از تحلیل کواریانس

محققی یک برنامه آزمایشی، برای افزایش پیشرفت تحصیلی دانش آموزان، در درس ریاضی اجرا کرد. ایشان، ابتدا، از بین 120 نفر از دانش آموزان پایه ششم یک مدرسه، تعداد 30 را به طور تصادفی انتخاب کرد. سپس یک پیش آزمون، مرتبط با مباحث ریاضی موجود در برنامه آزمایشی بر روی آنها اجرا کرد. در کنار این پیش آزمون، یک آزمون معتبر، استعداد ریاضی، بر روی آنها اجرا نمود. در مرحله بعد آزمودنی ها با یکدیگر همتاسازی شدند. به این ترتیب که محقق، نمرات پیش آزمون آزمودنی ها را از کم به زیاد مرتب کرد. سپس با توجه به این نمرات مرتب شده، آزمودنی ها را دو به دو، به طور تصادفی در یکی از گروه های کنترل یا آزمایش جایگزین کرد.

به این ترتیب، دو گروه 15 نفره همتا تشکیل شدند. یک گروه کنترل و گروه دیگر گروه آزمایش بود. محقق برنامه آزمایشی خود را در 16 جلسه، بر روی گروه آزمایش، اجرا نمود. گروه کنترل هیچ برنامه آزمایشی دریافت نکرد. بعد از اجرای آزمایش، پس آزمون، که دقیقاً همان سوالات پیش آزمون بود، بر روی همه آزمودنی ها ( گروه کنترل و گروه آزمایش)، اجرا گردید.

در مرحله بعد نمرات، وارد spss گردیدند. و این فرضیه که برنامه آزمایشی در پیشرفت تحصیلی دانش آموزان، در درس ریاضی موثر است، مورد آزمون قرار گرفت. روش آماری مورد استفاده، تحلیل کواریانس بود. در واقع، محقق، این موضوع را بررسی کرد که با حذف اثر متغیرهای همپراش، یعنی پیش آزمون و نیز استعداد ریاضی، آیا باز هم اثر برنامه آزمایشی معنی دار است یا خیر؟ نتایج مربوطه در ذیل ارائه شده اند.

نتایج تحلیل کواریانس

محقق، برای انجام تحلیل کواریانس، ابتدا پیش فرض های لازم را بررسی کرد. این پیش فرض ها، عبارتند از: نرمال بودن داده ها، یکسانی واریانس نمرات دو گروه و یکسانی شیب رگرسیون. این سه مورد از پیش فرض های اساسی، برای انجام تحلیل کواریانس هستند. در صورتی که پیش فرض ها، رعایت نشوند، نتایج تحلیل کواریانس، اعتباری ندارند. بنابراین لازم است، محقق پیش فرض ها را رعایت نماید.

بررسی نرمال بودن داده ها

جدول شماره 1 : نتایج آزمون های کلموگرو اسمیرنو و شاپیرو-ویلک در مورد نرمال بودن داده های تحقیق

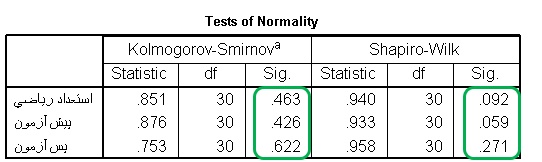
برای بررسی نرمال بودن داده ها از دو آزمون استفاده گردید. آزمون کلموگرو اسمیرنو و نیز آزمون شاپیرو- ویلک. با توجه به جدول بالا، سطوح معنی داری (sig) هر دو آزمون کلموگرو اسمیرنو و همینطور آزمون شاپیرو- ویلک، برای متغیر های استعداد تحصیلی، پیش آزمون و پس آزمون، از 0.05 بیشتر است. بنابراین شاخص های کلموگرو اسمیرنو و شاپیرو- ویلک، معنی دار نیستند. در نتیجه، با اطمینان، می توانیم بگوییم داده های تحقیق، نرمال هستند. و می توانیم از تحلیل کواریانس، استفاده کنیم.

بررسی یکسانی واریانس

جدول شماره 2 : نتایج آزمون لوین در مورد یکسانی واریانس های گروه های کنترل و آزمایش

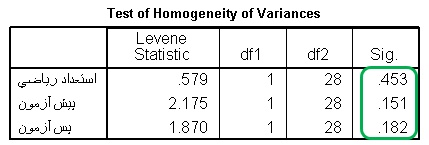
جدول بالا، نتایج آزمون لوین را نشان می دهد. براساس این جدول، سطوح معنی داری (sig)، برای هر سه متغیر، از 0.05 بیشتر است و معنی دار نیست. بنابراین با اطمینان، می توانیم بگوییم، شرط یکسانی واریانس ها برای انجام تحلیل کواریانس برقرار است.

بررسی همگنی شیب رگرسیون

جدول شماره3: تعامل متغیر مستقل و متغیرهای همپراش

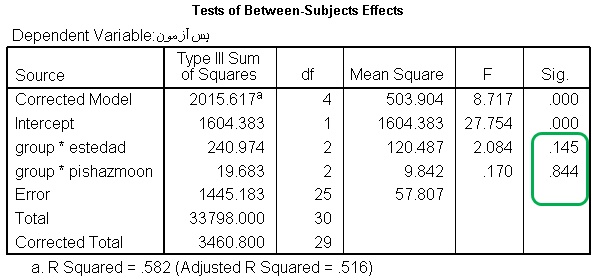
برای بررسی همگنی شیب رگرسیون، تعامل متغیر مستقل با متغیرهای همپراش، مورد بررسی، قرار گرفتند. با توجه به جدول بالا، سطوح معنی داری (sig)، تعامل متغیر مستقل (گروه)، با دو متغیر همپراش (استعداد ریاضی و پیش آزمون)، از 0.05 بیشتر است و معنی دار نیست. بنابراین با اطمینان، می توانیم بگوییم، شرط همگنی شیب رگرسیون، برای انجام تحلیل کواریانس برقرار است.

نتایج توصیفی

جدول شماره 4 : میانگین و انحراف معیار گروه های کنترل و آزمایش در آزمونهای استعداد ریاضی، پیش آزمون و پس آزمون

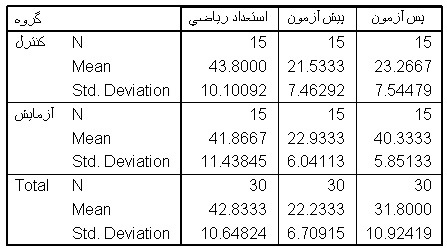
قبل از ارائه، نتایج ، تحلیل کواریانس، نتایج توصیفی را ارئه کردیم. تا مشخص شود، به لحاظ توصیفی، وضعیت نمرات چگونه است و چه تغییراتی داشته است. این نتایج، کمک می کنند، تا نتایج اصلی را بهتر تفسیر کنیم.

براساس جدول بالا، میانگین آزمودنی های گروه های کنترل و آزمایش، در آزمون استعداد ریاضی و پیش آزمون، با یکدیگر تفاوت قابل ملاحظه ای ندارند. پس دو گروه در این دو آزمون، با یکدیگر همتا هستند. ولی تفاوت میانگین آزمودنی های گروه های کنترل و آزمایش، در پس آزمون قابل ملاحظه است. به طوری که میانگین، آزمودنی های گروه آزمایش در پس آزمون، به طور قابل ملاحظه ای از میانگین پس آزمون گروه کنترل، بیشتر است.

نتایج اصلی تحلیل کواریانس

جدول شماره 5 : نتایج تحلیل کواریانس در مورد اثر بخشی برنامه آزمایشی در بهبود عملکرد ریاضی دانش آموزان

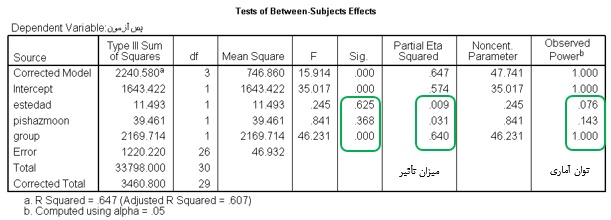
براساس جدول بالا، سطوح معنی داری (sig)، تأثیر دو متغیر همپراش (استعداد ریاضی و پیش آزمون)، از 0.05 بیشتر است و معنی دار نیست. بنابراین می توانیم، بگوییم، همپراش بودن این دو متغیر، معنی دار نیست. ولی به هر حال، در این تحلیل، اثر همپراشی آنها حذف گردیده است.

نیز براساس جدول بالا، سطح معنی داری (sig)، تأثیر متغیر مستقل (گروه کنترل و آزمایش)، از 0.05 کمتر است و بنابراین معنی دار است. به این معنی که، بعد از حذف اثر متغیرهای همپراش، باز هم تأثیر متغیر مستقل (گروه) معنی دار است. میزان تأثیر این متغیر 64 درصد و توان آماری آن معادل 1 می باشد.

با توجه به این نتیجه و نتایج توصیفی ارائه شده در جدول 4، می توانیم بگوییم، برنامه آزمایشی، موثر بوده است. و باعث شده، میزان یادگیری ریاضی گروه آزمایش، به طور معنی داری از میزان یادگیری گروه کنترل، بیشتر باشد.

سایر مطالب سایت

آنالیز واریانس

آنالیز واریانس چند راهه

تحلیل رگرسیون خطی

اندازه‌گیری‌های مکرر